2024年国考行测备考技巧:容斥问题
在行测考试中,容斥问题其实就是我们中学时代学习的集合,这种集合之间的交叉关系在行测考试中经常会出现,考察难度不大,但是很多同学容易被一些复杂的交叉关系搞得晕头转向,今天,我们再一次为大家梳理一下这类类问题,希望大家能在考试中取得好的成绩。
容斥问题,它其实就是一种计数问题,在计数中,当多个集合之间存在交叉时,我们需要将交叉重复部分减掉,从而求出总数。下面我们一起来看看容斥问题的重点题型。
一、重点题型:三者容斥
三者容斥就是研究三个集合之间的交叉关系,如下图所示。
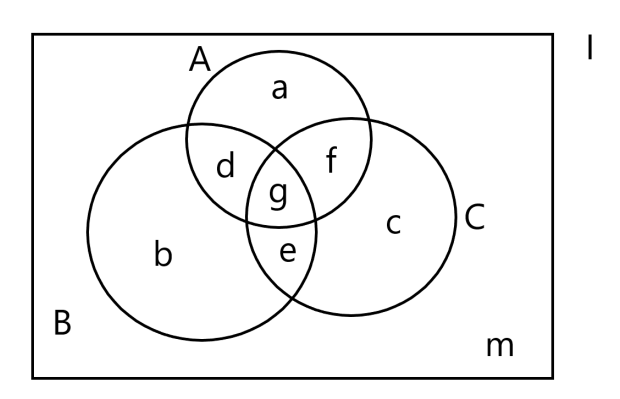
图中三个集合A、B、C
a:只属于A;b:只属于B;c:只属于C;
d:只属于A和B;e:只属于B和C;f:只属于A和C;
g:三者都属于;m:三者都不属于;
上图中的d、e、f、表示的是只属于两个集合,d、e、f、g则表示的是至少属于两个集合,我们在进行计数时,需要把重复的计数变为只数1次,或者说把重叠的面积变为一层,做到不重不漏,可先不考虑重复的情况,把包含于某集合中的所有对象的数目先计算出来,然后再把计数时重复计算的数目减掉,把遗漏的数目补上,使得计算结果既无重复也无遗漏。通过文氏图可推出计算公式:AUBUC=A+B+C-(d+e+f)-2g=I-m
二、例题训练
【例题1】为丰富职工业余文化生活,某单位组织了合唱、象棋、羽毛球三项活动,在该单位所有的职工中,参加合唱的有189人,参加象棋的有152人,参加羽毛球的有135人,只参加两种活动的有130人,三种活动都参加的有69人,不参加任何一种活动的44人,该单位一共有多少职工( )?
A.233 B.252 C.321 D.520
【答案】B
【解析】根据三者容斥的公式,该单位职工人数应为189+152+135-130-2×69=总-44人,总人数=252
因此,选择B选项。
【例题2】.某服装公司就消费者对红、黄、蓝三种颜色的偏好情况进行市场调查,共抽取了40名消费者,发现其中有20人喜欢红色、20人喜欢黄色、15人喜欢蓝色,至少喜欢两种颜色的有19人,喜欢三种颜色的有3人,问三种颜色都不喜欢的有几人?
A.1 B.3 C.5 D.7
【答案】D
【解析】至少喜欢两种色的有19人・喜欢三种色的有3人,则喜欢两种色的有19-3=16人。离欢红、黄、蓝三色的人数相加其中喜欢两种色的被重复计算一次,喜欢三种颜色的被重复计算两次,至少喜欢一种颜色的有20+20+15-16-2x3=33人。三种颜色都不喜欢的有40-33=7人。
因此,选择D选项。
【例题3】.某专业有学生50人,现开设有甲、乙、丙三门选修课。有40人选修甲课程,36人选修乙课程,30人选修两课程,兼选甲、乙两门课程的有28人,兼选甲、丙两门课程的有26人,兼选乙、丙两门课程的有24人,甲、乙、丙三门课程均选的有20人,问三门课程均未选的有多少人?
A.1人 B.2人 C.3人 D.4人
【答案】B
【解析】设三门课均未选的有m人,根据三者容斥原理可得40+36+30-28-26-24+20=50-m,解得m=2,即三门都没选的有2人。
因此,选择B选项。
到此,相信各位同学已经能够理解和掌握了容斥问题的解题原则以及解题方法,也相信各位同学在今后的考试中能逐一击破。
在行测考试中,容斥问题其实就是我们中学时代学习的集合,这种集合之间的交叉关系在行测考试中经常会出现,考察难度不大,但是很多同学容易被一些复杂的交叉关系搞得晕头转向,今天,我们再一次为大家梳理一下这类类问题,希望大家能在考试中取得好的成绩。
容斥问题,它其实就是一种计数问题,在计数中,当多个集合之间存在交叉时,我们需要将交叉重复部分减掉,从而求出总数。下面我们一起来看看容斥问题的重点题型。
一、重点题型:三者容斥
三者容斥就是研究三个集合之间的交叉关系,如下图所示。

图中三个集合A、B、C
a:只属于A;b:只属于B;c:只属于C;
d:只属于A和B;e:只属于B和C;f:只属于A和C;
g:三者都属于;m:三者都不属于;
上图中的d、e、f、表示的是只属于两个集合,d、e、f、g则表示的是至少属于两个集合,我们在进行计数时,需要把重复的计数变为只数1次,或者说把重叠的面积变为一层,做到不重不漏,可先不考虑重复的情况,把包含于某集合中的所有对象的数目先计算出来,然后再把计数时重复计算的数目减掉,把遗漏的数目补上,使得计算结果既无重复也无遗漏。通过文氏图可推出计算公式:AUBUC=A+B+C-(d+e+f)-2g=I-m
二、例题训练
【例题1】为丰富职工业余文化生活,某单位组织了合唱、象棋、羽毛球三项活动,在该单位所有的职工中,参加合唱的有189人,参加象棋的有152人,参加羽毛球的有135人,只参加两种活动的有130人,三种活动都参加的有69人,不参加任何一种活动的44人,该单位一共有多少职工( )?
A.233 B.252 C.321 D.520
【答案】B
【解析】根据三者容斥的公式,该单位职工人数应为189+152+135-130-2×69=总-44人,总人数=252
因此,选择B选项。
【例题2】.某服装公司就消费者对红、黄、蓝三种颜色的偏好情况进行市场调查,共抽取了40名消费者,发现其中有20人喜欢红色、20人喜欢黄色、15人喜欢蓝色,至少喜欢两种颜色的有19人,喜欢三种颜色的有3人,问三种颜色都不喜欢的有几人?
A.1 B.3 C.5 D.7
【答案】D
【解析】至少喜欢两种色的有19人・喜欢三种色的有3人,则喜欢两种色的有19-3=16人。离欢红、黄、蓝三色的人数相加其中喜欢两种色的被重复计算一次,喜欢三种颜色的被重复计算两次,至少喜欢一种颜色的有20+20+15-16-2x3=33人。三种颜色都不喜欢的有40-33=7人。
因此,选择D选项。
【例题3】.某专业有学生50人,现开设有甲、乙、丙三门选修课。有40人选修甲课程,36人选修乙课程,30人选修两课程,兼选甲、乙两门课程的有28人,兼选甲、丙两门课程的有26人,兼选乙、丙两门课程的有24人,甲、乙、丙三门课程均选的有20人,问三门课程均未选的有多少人?
A.1人 B.2人 C.3人 D.4人
【答案】B
【解析】设三门课均未选的有m人,根据三者容斥原理可得40+36+30-28-26-24+20=50-m,解得m=2,即三门都没选的有2人。
因此,选择B选项。
到此,相信各位同学已经能够理解和掌握了容斥问题的解题原则以及解题方法,也相信各位同学在今后的考试中能逐一击破。
声明:本网站部分内容来源于网络搜集及网友投稿,由本站编辑整理发布,仅用于学习交流使用,非盈利目的,如涉及侵权请联系本站管理员进行删除或修改。





