一、看选项猜题
(1)根据倍数关系猜题
①题型特征:选项与题干存在对应的倍数关系。
②猜题思路:按照题干逻辑把选项与题干主体进行对应,根据题目问题猜答案。
例题:2018上海
大小两个玻璃瓶装着芝麻,如果将小瓶子里的芝麻全部倒入大瓶子,大瓶子还可以装45克;如果将大瓶子里的芝麻倒入小瓶子,大瓶子里还剩下455克。已知大瓶子的容积是小瓶子的2倍,则大瓶子最多可装芝麻多少克?
A.1000
B.850
C.750
D.500
【答案】A
※猜题思路:根据题干“大瓶子的容积是小瓶子的2倍”,观察选项,A项(1000)恰好是D项(500)的2倍,猜测出题人设置D项为小瓶子容积、A项为大瓶子容积,猜测本题的答案为A项。
【拓展】倍数关系除了题目中明确给出外,还可能是题目的隐含条件或者知识点中包含的倍数关系,例如:往返的总路程是单程距离的2倍,直径是半径的2倍。
“
(2)根据和差关系猜题
①题型特征:选项与题干存在对应的和差关系。
②猜题思路:按照题干逻辑把选项与题干主体进行对应,根据题目问题猜答案。
例题:2020联考
春节期间,省图书馆邀请多位书法老师免费为读者书写春联。现场书写的春联中有188副不是刘老师书写的,有219副不是陈老师书写的,刘、陈两位老师今年一共书写了311副春联。问陈老师今年一共书写了多少副春联?
A.208
B.171
C.140
D.126
【答案】C
※猜题思路:根据题干“刘、陈两位老师今年一共书写了311副春联”,观察选项,B项(171)+C项(140)=311,结合“有188副不是刘老师书写的,有219副不是陈老师书写的”,故陈老师写得少,选择少的,猜测本题的答案为C项。
二、几何猜题
GUESS
“
(1)看选项结构
①题型特征:四个选项代数式结构差异明显,例如是否包含π、是否有加减运算等。
②猜题思路:根据图形面积的计算逻辑猜答案。
例题:2019广东
某小区规划建设一块边长为10米的正方形绿地。如图所示,以绿地的2个顶点为圆心,边长为半径分别作扇形,把绿地划分为不同的区域。小区现准备在图中阴影部分种植杜鹃,则杜鹃种植面积为多少平方米?

A. 100-25π
B. 200-35π
C. 200-50π
D. 100π-100
【答案】A
※猜题思路:读题可知,阴影部分总面积=正方形面积-扇形面积(即不带π的数-有π的数),且正方形面积为平方数。观察选项,只有A项符合,猜测本题答案为A项。
“
(2)看图像估算
①题型特征:题干给出较为标准的图形。
②猜题思路:根据量尺测量或目测,猜答案。
例题:2017联考
某电信公司推出两种手机收费方式:A种方式是月租20元,B种方式是月租0元。一个月的本地网内通话时间t(分钟)与电话费S(元)的函数关系如图所示,当通话150分钟时,这两种方式的电话费相差:
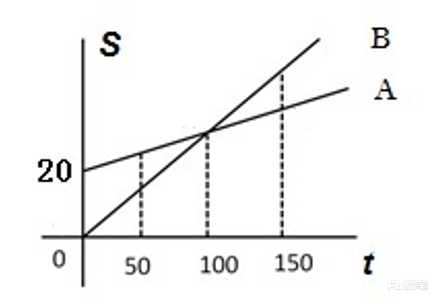
A.10元
B.15元
C.20元
D.30元
【答案】A
※猜题思路:问AB之间在150分钟处的差值,观察图形,S轴有参考长度20,观察两段长度的关系,近似为一半关系,猜测本题答案为A项。




