利用插空法解排列组合题-2025国家公务员考试行测解题技巧
排列组合类题目一直是行测数量关系中的高频考点,近年来,基本每年都会出现一道或者两道题,而排列组合专项又因其题目难度大而令许多考生望而生畏。但虽然排列组合专项难,技巧性却很强,接下来为各位考生介绍在排列组合解题中使用比较频繁的方法,即插空法。
【例1】某学习平台的学习内容由观看视频、阅读文章、收藏分享、论坛交流、考试答题五个部分组成。某学员要先后学完这五个部分,若观看视频和阅读文章不能连续进行,该学员学习顺序的选择有( )种。
A.24
B.72
C.96
D.120
答案:B
【解析】①先处理除不相邻元素以外的部分,再找出能够插入的空位;
②将不相邻元素插入到不同空位中;
③做题时注意元素之间是否有顺序要求。
③在①和②的过程中体现。
例题1中,①观看视频和阅读文章不能连续进行,余下的为收藏分享、论坛交流、考试答题,共3个部分,因为要先后学完这几部分,改变顺序对结果有影响,用排列数(对③的体现),共
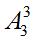
种,3个部分共形成4个可以插入的空位,②将观看视频、阅读文章插入时,改变顺序对结果有影响,用排列数(对③的体现),共
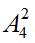
种。
以上两个环节为分步的过程,使用分步相乘,所求学习顺序有
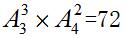
种,故本题选B。
【例2】由数字1、2、3、4、5、6、7组成无重复数字的七位数,求三个偶数互不相邻的七位数的个数?
A.360
B.720
C.1440
D.2880
答案:C
【解析】问题中出现三个偶数互不相邻,考虑用插空法解题。首先将除三个偶数外的数字1、3、5、7进行排序,有
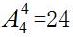
种不同的排法;这4个数字会产生5个空隙,从5个空隙中选出3个,有
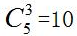
种不同的排法;最后将三个偶数进行排序,有
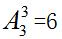
种不同的排法,所以总的排法有24×10×6=1440种,故选择C选项。
【例3】把12棵同样的松树和6棵同样的柏树种植在道路两侧,每侧种植9棵,要求每侧的柏树数量相等且不相邻,且道路起点和终点处两侧种植的都必须是松树。问有多少种不同的种植方法?
A.36
B.50
C.100
D.400
答案:C
【解析】由题意,公路两边各6棵松树和3棵柏树,道路起点和终点处两侧种植的都必须是松树,那么中间有5个空,由于柏树要求互不相邻,故从5个空中选出3个空栽种柏树即可。故每一边的种植方式为
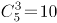
,故有10×10=100种不同的种植方法。故正确答案为C。
最后给大家总结一下插空法:插空法主要适用于要求“不相邻”、“不排在一起”的排列组合题目。此外,在使用插孔法的时候我们要注意所使用对象是谁,如果对象为人,那么可能注意顺序,如果对象为“路灯”、“树”或者其他注明是相同的对象,那么就不必先排列剩余元素了。在使用插空法解答题目的时候,还要特别注意两侧的情况,有的时候我们所要放入空中的元素,不能放在所剩余元素的两侧,大家读题的时候,千万要细心。
排列组合类题目一直是行测数量关系中的高频考点,近年来,基本每年都会出现一道或者两道题,而排列组合专项又因其题目难度大而令许多考生望而生畏。但虽然排列组合专项难,技巧性却很强,接下来为各位考生介绍在排列组合解题中使用比较频繁的方法,即插空法。
【例1】某学习平台的学习内容由观看视频、阅读文章、收藏分享、论坛交流、考试答题五个部分组成。某学员要先后学完这五个部分,若观看视频和阅读文章不能连续进行,该学员学习顺序的选择有( )种。
A.24
B.72
C.96
D.120
答案:B
【解析】①先处理除不相邻元素以外的部分,再找出能够插入的空位;
②将不相邻元素插入到不同空位中;
③做题时注意元素之间是否有顺序要求。
③在①和②的过程中体现。
例题1中,①观看视频和阅读文章不能连续进行,余下的为收藏分享、论坛交流、考试答题,共3个部分,因为要先后学完这几部分,改变顺序对结果有影响,用排列数(对③的体现),共
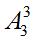
种,3个部分共形成4个可以插入的空位,②将观看视频、阅读文章插入时,改变顺序对结果有影响,用排列数(对③的体现),共
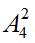
种。
以上两个环节为分步的过程,使用分步相乘,所求学习顺序有
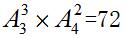
种,故本题选B。
【例2】由数字1、2、3、4、5、6、7组成无重复数字的七位数,求三个偶数互不相邻的七位数的个数?
A.360
B.720
C.1440
D.2880
答案:C
【解析】问题中出现三个偶数互不相邻,考虑用插空法解题。首先将除三个偶数外的数字1、3、5、7进行排序,有
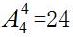
种不同的排法;这4个数字会产生5个空隙,从5个空隙中选出3个,有
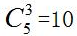
种不同的排法;最后将三个偶数进行排序,有
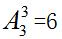
种不同的排法,所以总的排法有24×10×6=1440种,故选择C选项。
【例3】把12棵同样的松树和6棵同样的柏树种植在道路两侧,每侧种植9棵,要求每侧的柏树数量相等且不相邻,且道路起点和终点处两侧种植的都必须是松树。问有多少种不同的种植方法?
A.36
B.50
C.100
D.400
答案:C
【解析】由题意,公路两边各6棵松树和3棵柏树,道路起点和终点处两侧种植的都必须是松树,那么中间有5个空,由于柏树要求互不相邻,故从5个空中选出3个空栽种柏树即可。故每一边的种植方式为
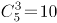
,故有10×10=100种不同的种植方法。故正确答案为C。
最后给大家总结一下插空法:插空法主要适用于要求“不相邻”、“不排在一起”的排列组合题目。此外,在使用插孔法的时候我们要注意所使用对象是谁,如果对象为人,那么可能注意顺序,如果对象为“路灯”、“树”或者其他注明是相同的对象,那么就不必先排列剩余元素了。在使用插空法解答题目的时候,还要特别注意两侧的情况,有的时候我们所要放入空中的元素,不能放在所剩余元素的两侧,大家读题的时候,千万要细心。
声明:本网站部分内容来源于网络搜集及网友投稿,由本站编辑整理发布,仅用于学习交流使用,非盈利目的,如涉及侵权请联系本站管理员进行删除或修改。
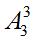 种,3个部分共形成4个可以插入的空位,②将观看视频、阅读文章插入时,改变顺序对结果有影响,用排列数(对③的体现),共
种,3个部分共形成4个可以插入的空位,②将观看视频、阅读文章插入时,改变顺序对结果有影响,用排列数(对③的体现),共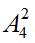 种。
种。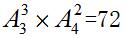 种,故本题选B。
种,故本题选B。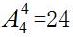 种不同的排法;这4个数字会产生5个空隙,从5个空隙中选出3个,有
种不同的排法;这4个数字会产生5个空隙,从5个空隙中选出3个,有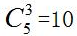 种不同的排法;最后将三个偶数进行排序,有
种不同的排法;最后将三个偶数进行排序,有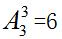 种不同的排法,所以总的排法有24×10×6=1440种,故选择C选项。
种不同的排法,所以总的排法有24×10×6=1440种,故选择C选项。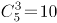 ,故有10×10=100种不同的种植方法。故正确答案为C。
,故有10×10=100种不同的种植方法。故正确答案为C。



