数学学科知识点--小学数学应用题(一)
一、工程问题
1.工程问题基本概念
基本数量关系:工作效率×工作时间=工作总量。
基本思路:设工作总量为“1”,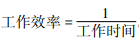 。
。
2.水管问题
从数学的角度来看,水管问题与工程问题是一样的,水池的注水或排水相当于一项工程,注水量或排水量就是工作量,单位时间里的注水量或排水量就是工作效率,至于注入与排出的问题,可看作是工作量的加减。因此,水管问题与工程问题的解题思路基本相同。
3.牛吃草问题
对于同一片草地,由于每头牛吃草的速度不变,所以牛头数越多(少),草能够吃的天数越少(多)。假设每头牛每天吃草的速度为“1”份,由此我们可以总结出解决牛吃草问题常用到的四个基本公式,分别是:
①草的生长速度=某时间段内草生长的量+对应的天数=(草能够吃的较多天数×相应的牛头数-草能够吃的较少天数×相应的牛头数)+天数差;
②原有草量=牛吃的总量-这段时间新生长的草的量=牛头数x吃的天数-草的生长速度x吃的天数;
③吃的天数=草量÷草每天减少的量=原有草量÷(牛头数-草的生长速度);
④牛头数=原有草量÷吃的天数+草的生长速度。
一、工程问题
1.工程问题基本概念
基本数量关系:工作效率×工作时间=工作总量。
基本思路:设工作总量为“1”,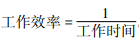 。
。
2.水管问题
从数学的角度来看,水管问题与工程问题是一样的,水池的注水或排水相当于一项工程,注水量或排水量就是工作量,单位时间里的注水量或排水量就是工作效率,至于注入与排出的问题,可看作是工作量的加减。因此,水管问题与工程问题的解题思路基本相同。
3.牛吃草问题
对于同一片草地,由于每头牛吃草的速度不变,所以牛头数越多(少),草能够吃的天数越少(多)。假设每头牛每天吃草的速度为“1”份,由此我们可以总结出解决牛吃草问题常用到的四个基本公式,分别是:
①草的生长速度=某时间段内草生长的量+对应的天数=(草能够吃的较多天数×相应的牛头数-草能够吃的较少天数×相应的牛头数)+天数差;
②原有草量=牛吃的总量-这段时间新生长的草的量=牛头数x吃的天数-草的生长速度x吃的天数;
③吃的天数=草量÷草每天减少的量=原有草量÷(牛头数-草的生长速度);
④牛头数=原有草量÷吃的天数+草的生长速度。
声明:本网站部分内容来源于网络搜集及网友投稿,由本站编辑整理发布,仅用于学习交流使用,非盈利目的,如涉及侵权请联系本站管理员进行删除或修改。
 。
。



